Red-Black tree, in English

People say that “If I can’t coding it, then I don’t understand it”, so I spend some days to implement the red-black tree. Most people feel confusing when learning the rules of RB-tree insertion and deletion first time just like me, I hope this blog can help you understand it better.

Let’s revise binary search tree (BST) first, some confusion explanation in RB-tree actually came from the convention in BST.

BST properties:

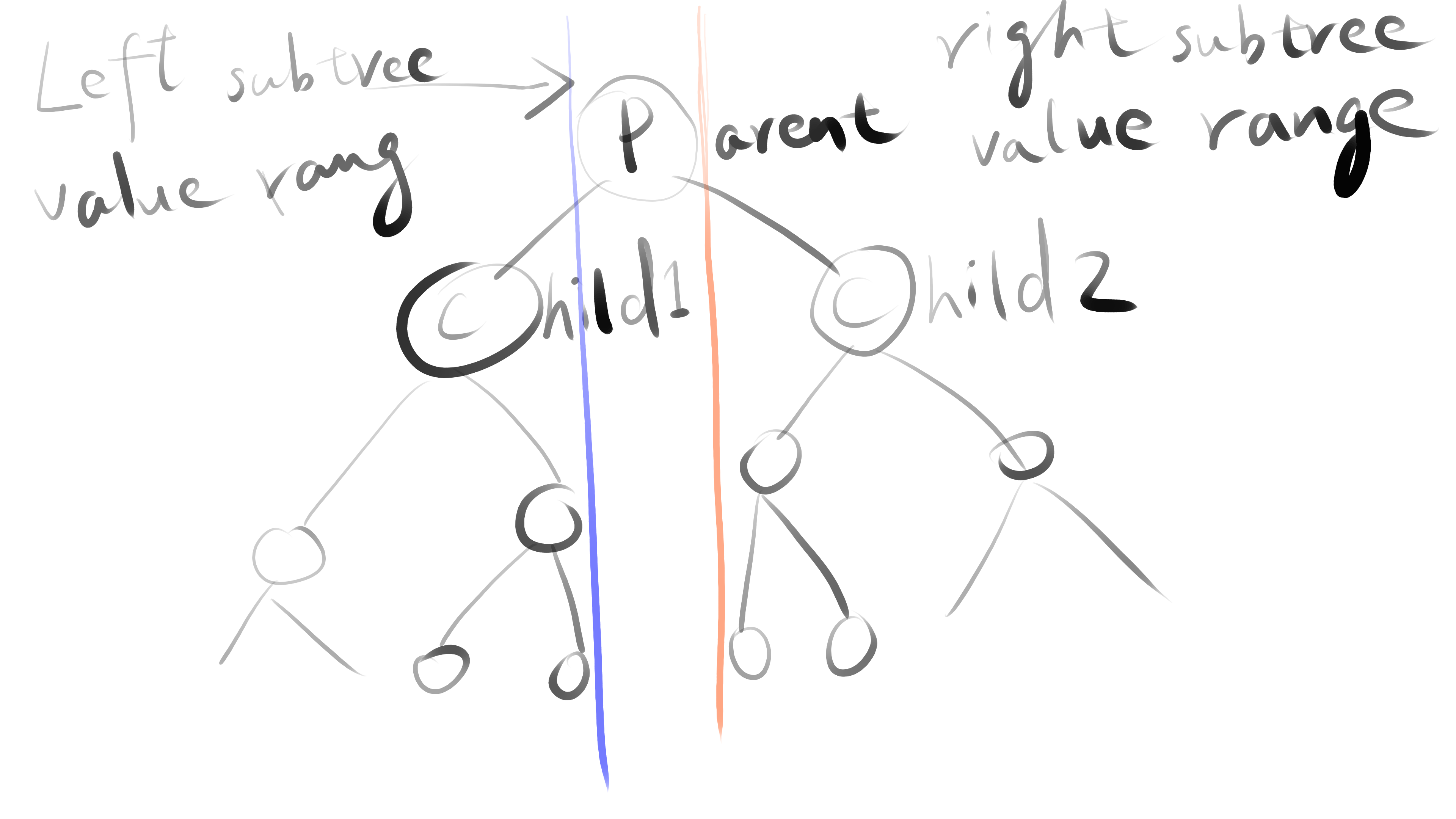
parent node value is greater than any node of left-child sub-tree, and less than any node of right-child sub-tree

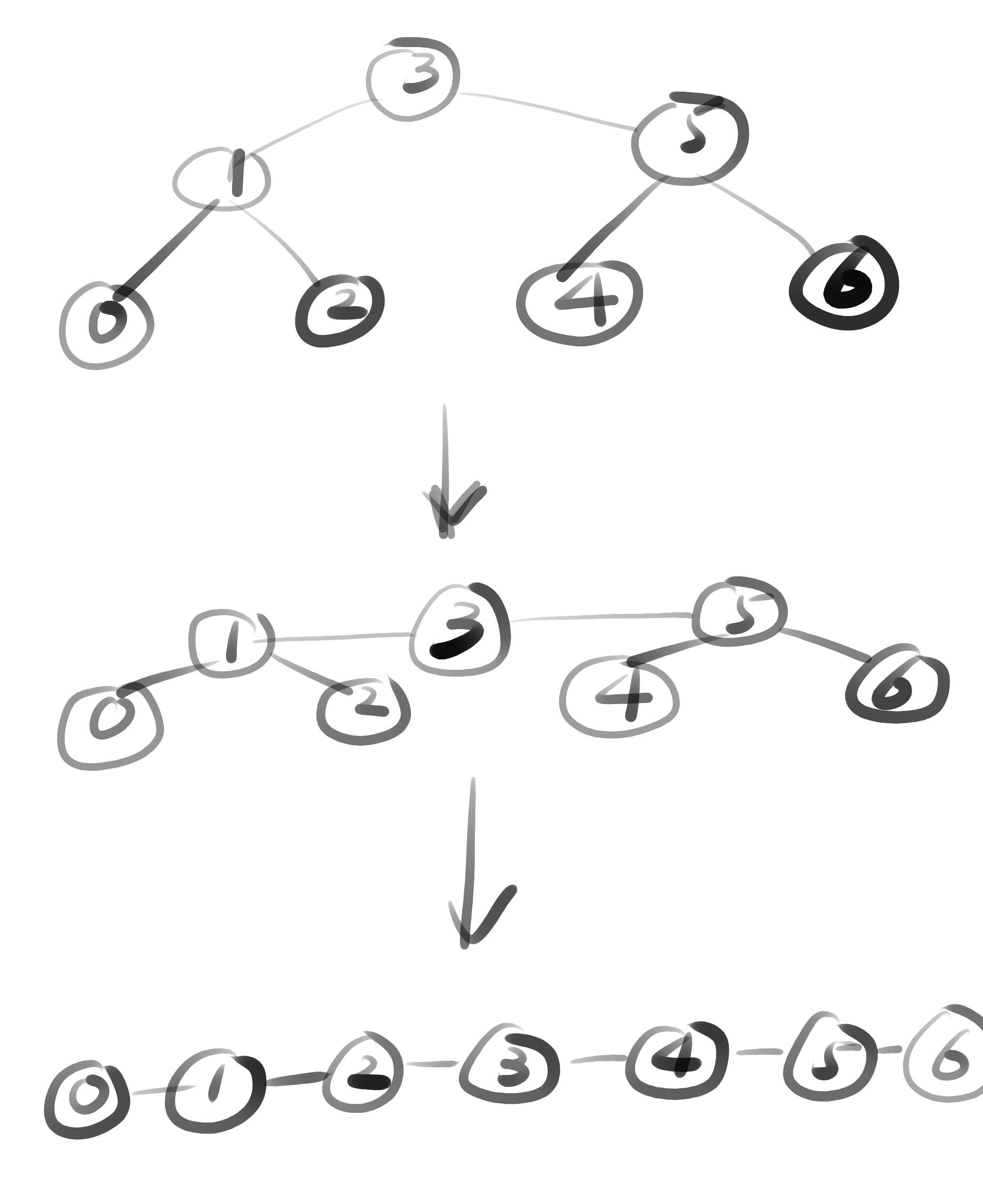
if “flatten” the BST, every value stay at their original horizontal position, then this will form a sorted list

the in-order successor element of a node, is the left-most node of right-child sub-tree, because it’s the right side most near node after flatten
new inserted node (new unique value), will always insert as leaf node, say, replace a null child, it will never ‘replace’ any existing node, or being the third child of some node

most important rule (to help understanding RB-tree deletion): when remove a value, it never remove the node directly, we always swap it with in-order successor, then we remove the replaced node

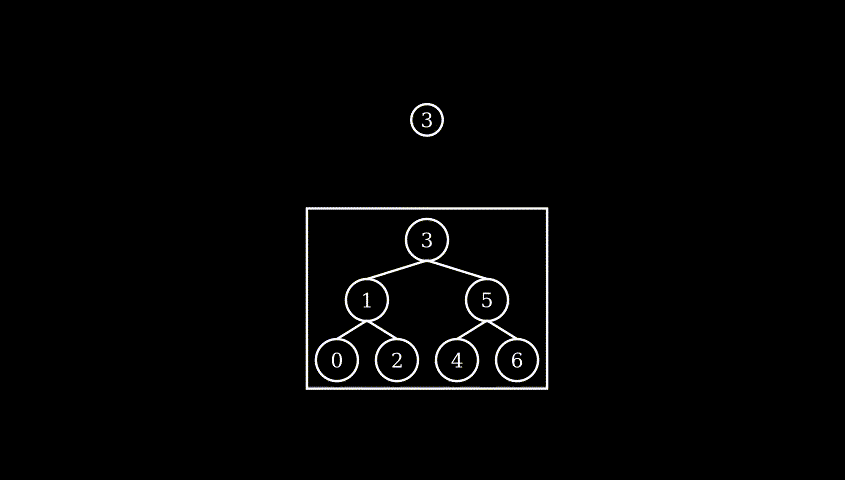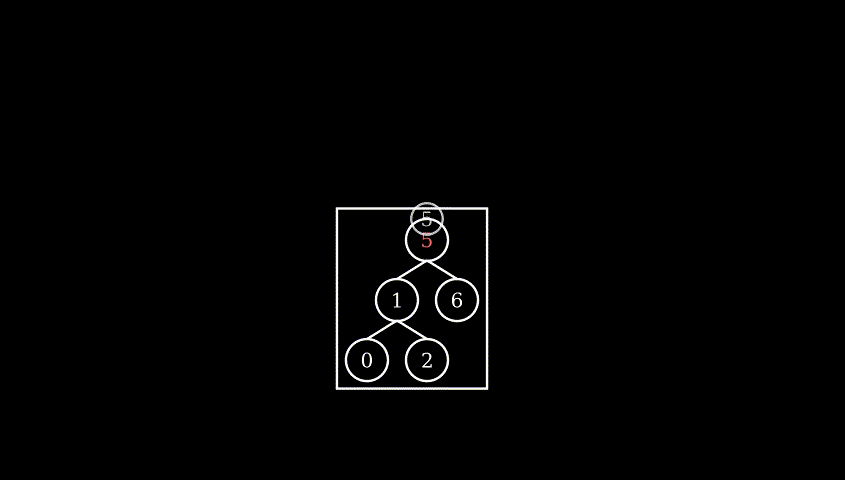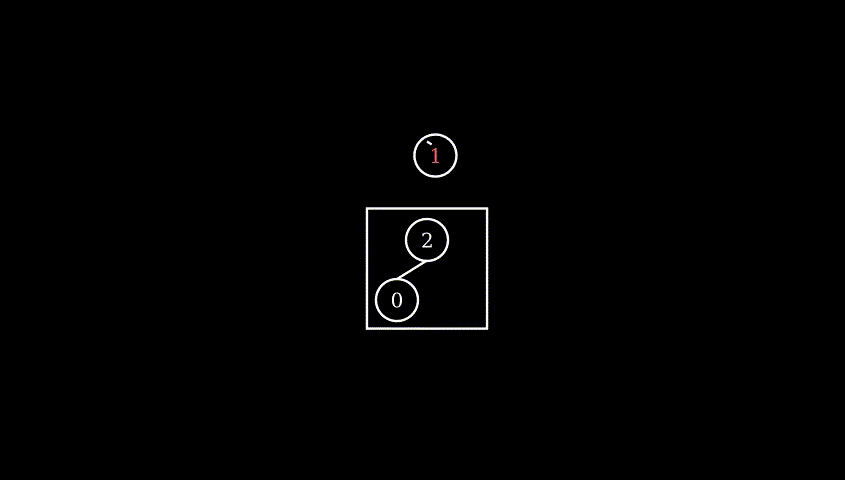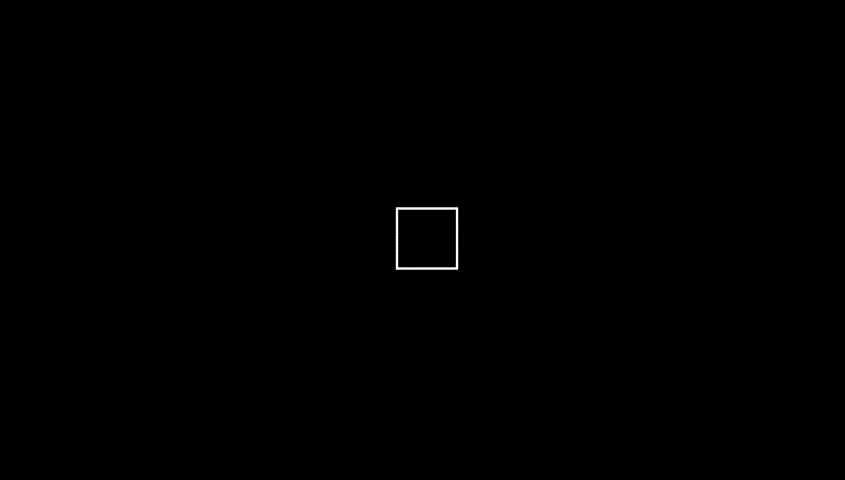since the in-order successor is the left-most node, so it either has only one right child, or no children at all (otherwise its left child will be more left )

you can use child as the new ROOT to construct valid BST by only adjust parent,sibling and nephew relationship, other part of trees structure won’t change, this is called rotation

example: rotate at leaf node

example: rotate with sub-trees

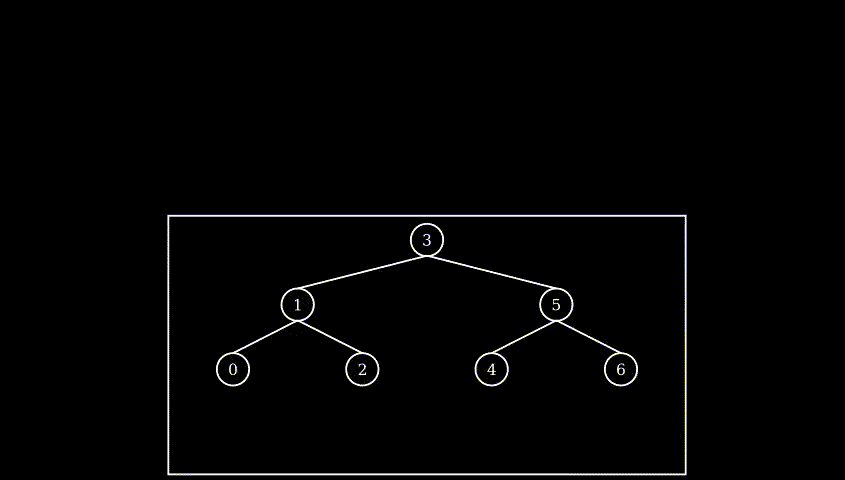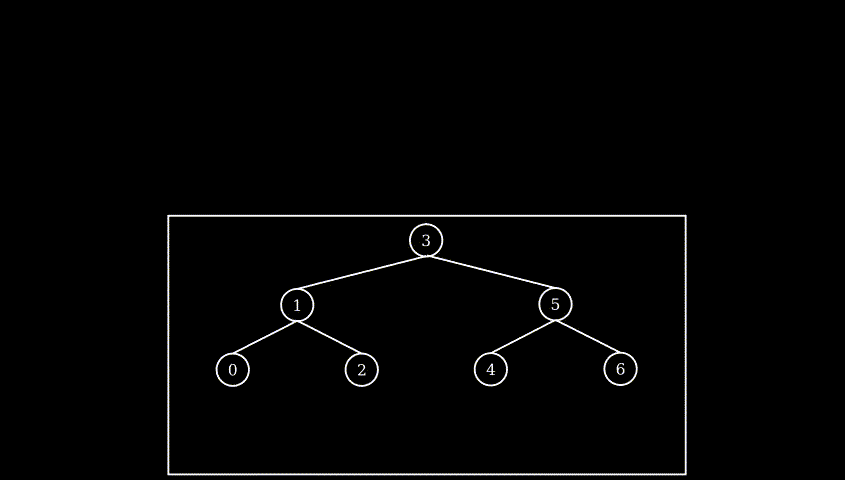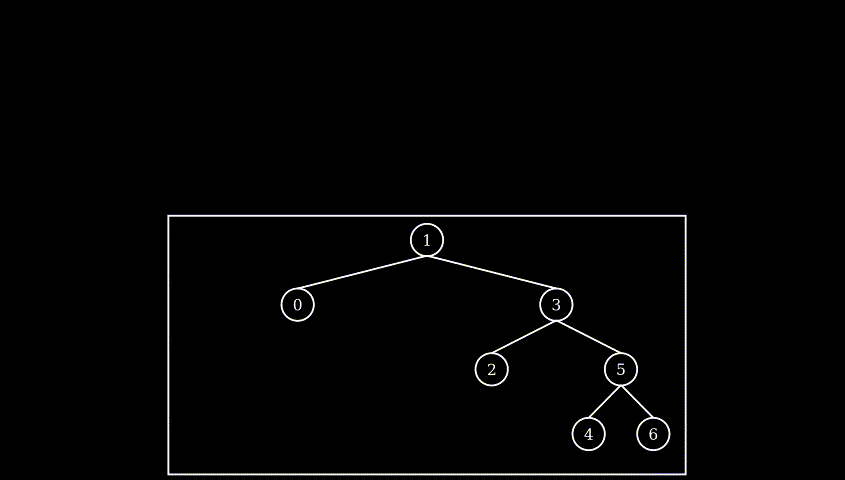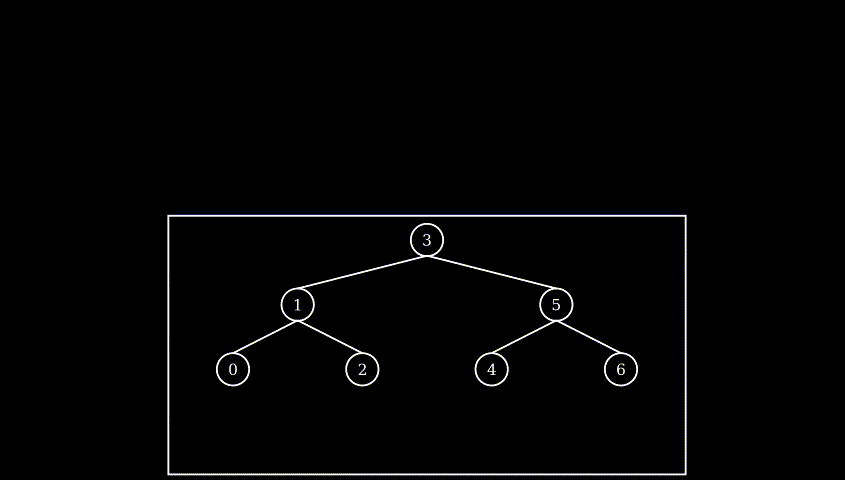
note: during rotation, the horizontal relative position never changed, whole BST flatten to exactly same ordered list, only relationship around the pivot node (children and grandson) changed, other part of tree keeps exactly same structure

Now let’s get into RB-tree. Most references and blogs focus on precise definition and operation rules, leave the explanation in pure math text description, but I’ll explain it by inaccurate ‘idea’ first, actual definition and rules second, keep the reason ‘why we’re dong this’ in mind first makes it much easier to understand the details. (please note the list number also different to other references)

why mark node with Red/Black color? It’s a way to help BST avoiding decay to linear list

BST decay to list example
how to avoid BST decay to linear list? by enforcing longest path shorter than 2 times of shortest path
why BST requires no consequent red nodes? This enforce along any path, RED nodes number won’t exceed BLACK nodes + 1, if we requires ROOT always black, then RED <= BLACK (following discussion omit ROOT must be black rule, doesn’t affect most result except longest path length can be 2 times of shortest + 1)
why BST requires equal black height? Combined with rule 3, we have

  RED(max) <= BLACK
  longest path depth L = BLACK + RED(max)
  shortest path depth S = BLACK
  then 
  L <= S + S 

this assume RB-Tree won’t decay to linear list

according to these rules, we know that:

property 1 : RED node doesn’t contribute to black height, so if modification (insert or delete) is red node, it will be the most simplest case

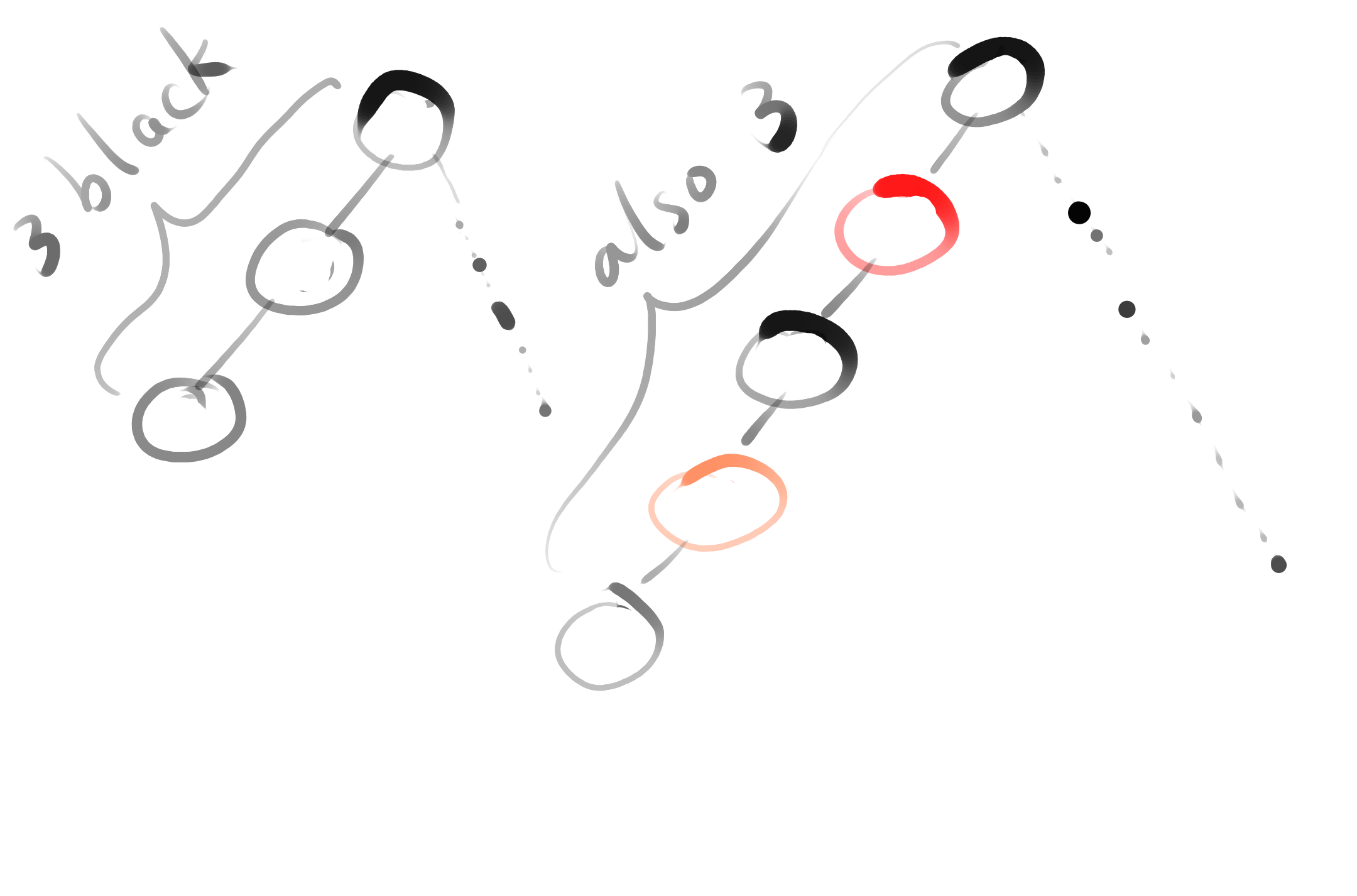
property 2 : if we have two nodes, then parent must be Black, and child must be RED (otherwise the black height won’t be equal)

property 3: if we have three nodes (as subtree), it can only be

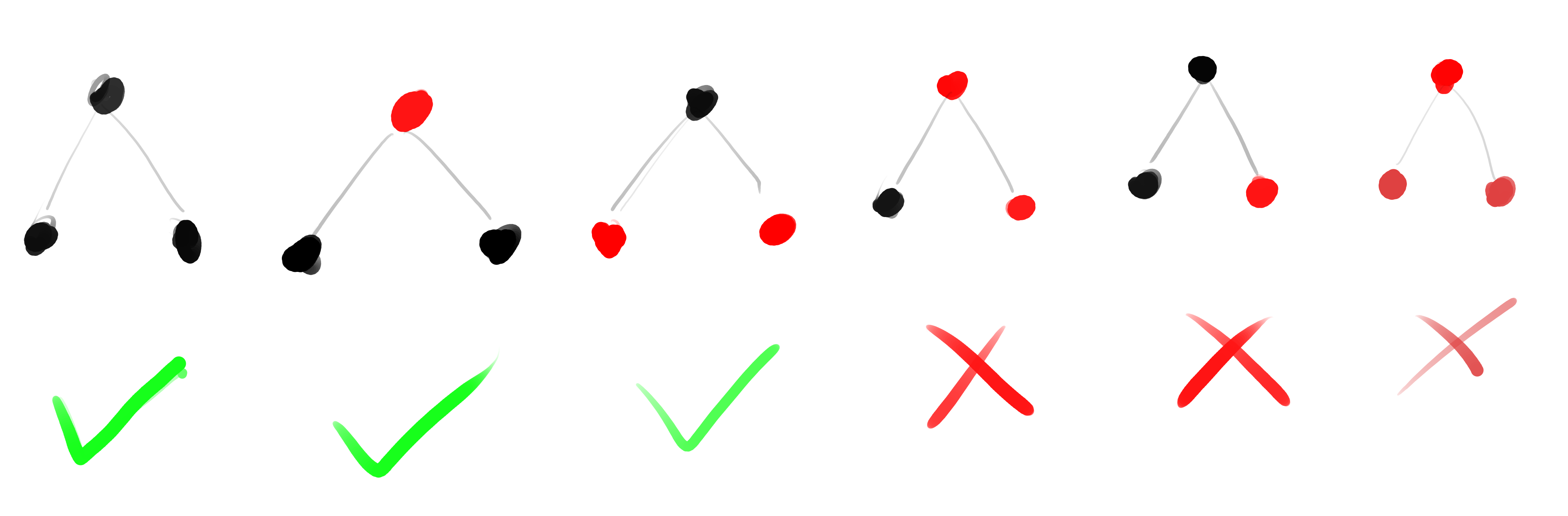
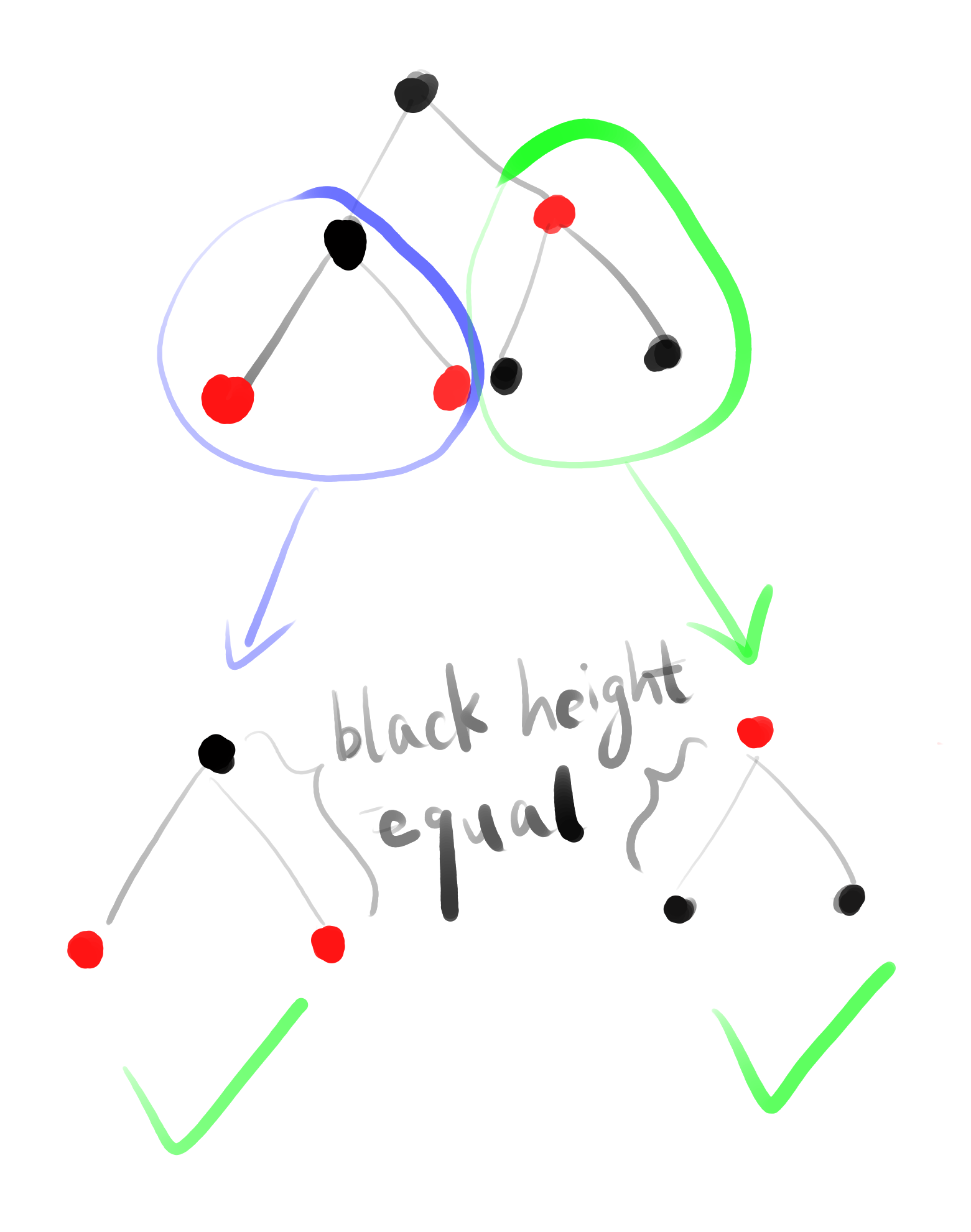
property 4: all path black height equal, since two child sub-tree share same root node, their sub-tree black height are also equal. And no matter which color the root node being changed to, both sub-tree still have same black height. any sub-tree of a valid RB-Tree, is also valid RB-Tree (note we don’t require root must be black)

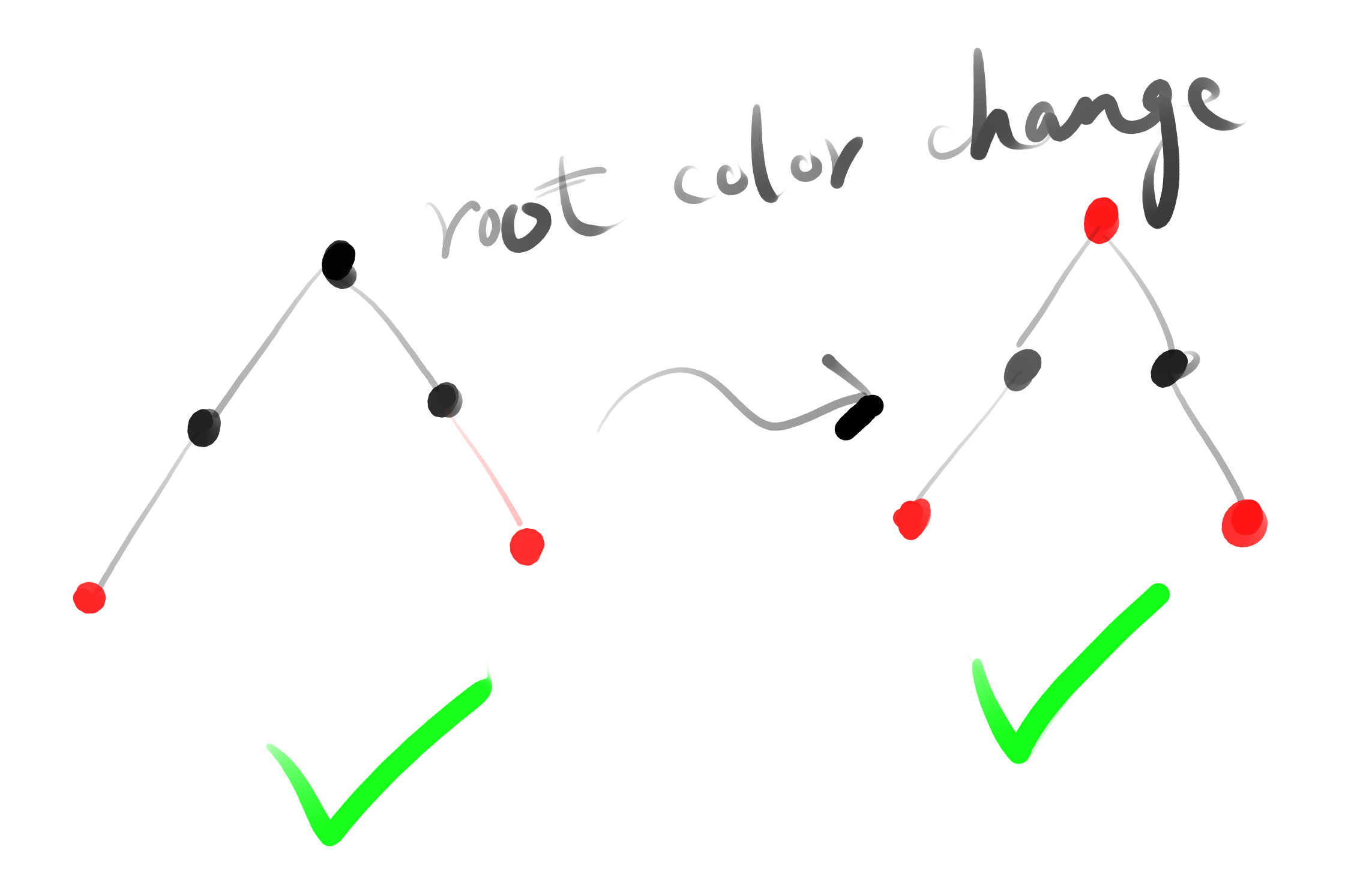
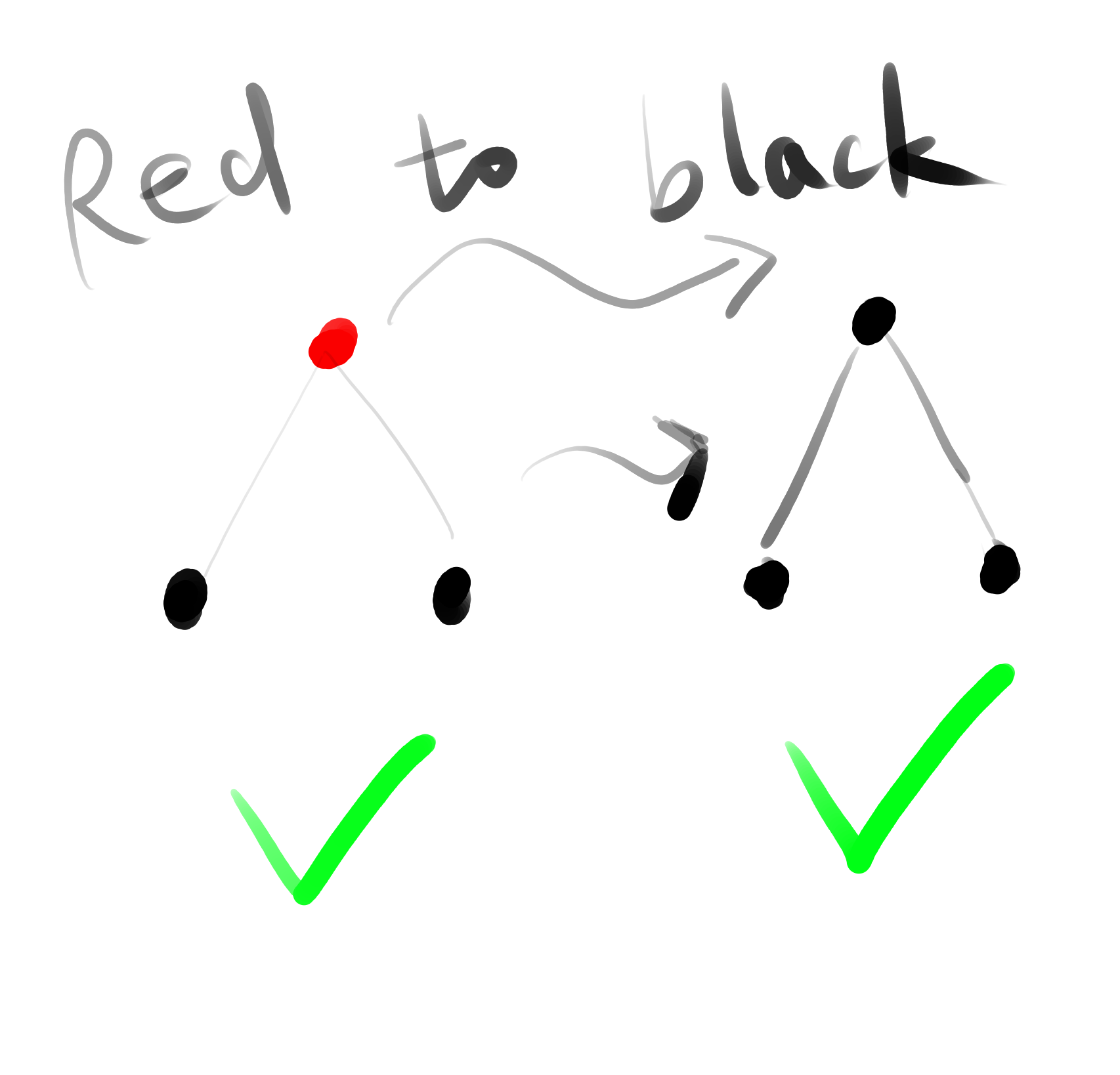
property 5: turn RED-NODE to BLACK won’t introduce new consequent red condition, also won’t make the sub-tree invalid RB-Tree

insertion

idea: keep the goal in mind before getting into details, an valid RB-Tree will be valid after insertion if:

black height equal for all path
no consequent red

so our insertion strategy will be:

not change black height, so new inserted node should be RED (RBT property 1, RED doesn’t contribute to black height),
if we have consequent RED situation, try find nearby black nodes(parent/sibling/uncle), see if we can re-arrange them to move the ‘extra red’ in-between black nodes (while maintaining exactly same black height)
if 2 is not possible, then we try to make larger sub-tree valid RB-Tree and push the extra red color upwards, expect we can resolve it at higher level

by applying this idea, we will either fixing the violation at some step, or making higher and higher sub-tree valid until we reach root, so whole tree fixed. RBTree property 4 also playing important rule here: for an valid RB-Tree, any sub-tree is also valid RB-Tree, left-right child will have same black height

insert new Node as RED.
if the parent is BLACK, then we already done (property 1)
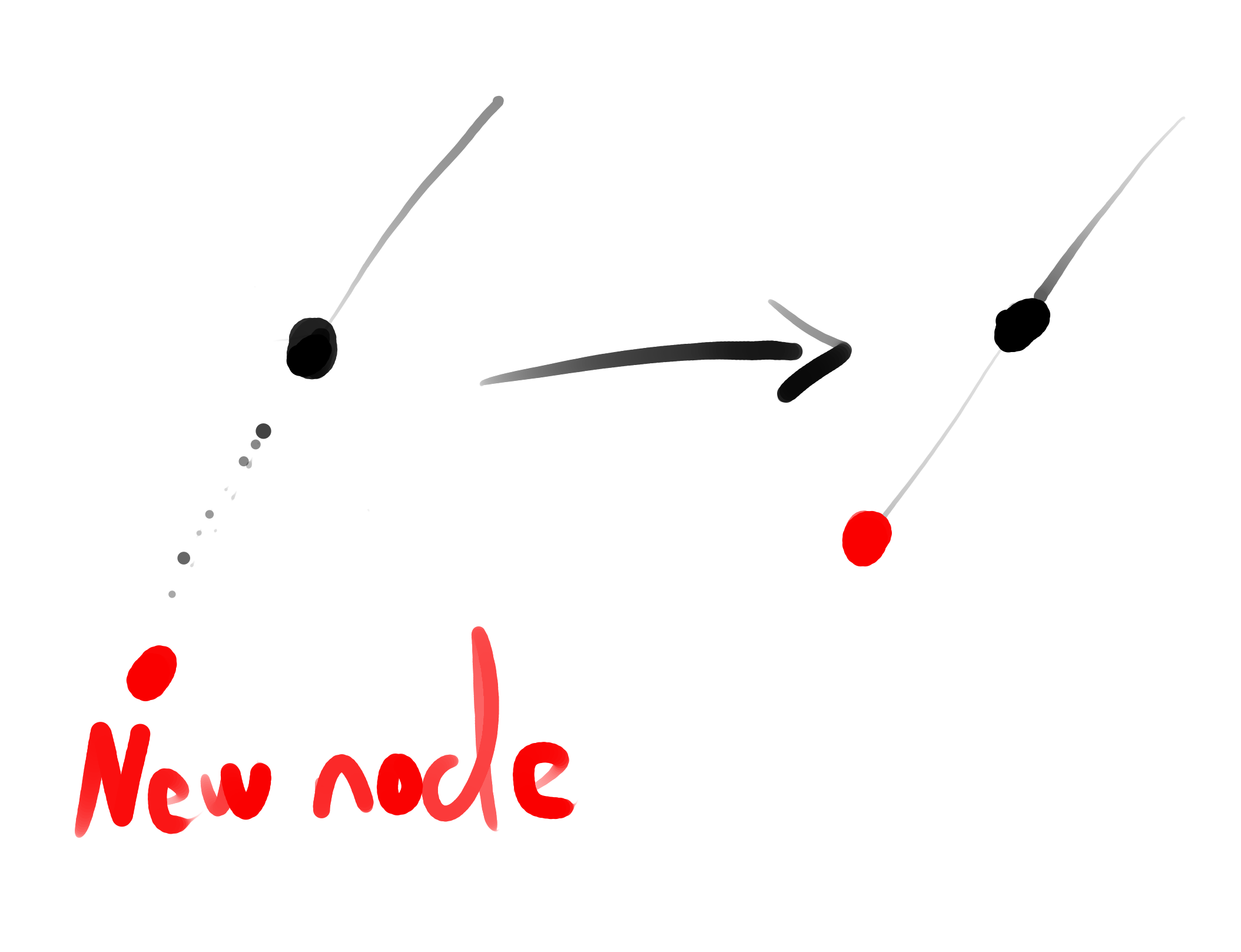
if the parent is RED, then it must contains no children before insertion (see two nodes all possible condition), so possible structures are (position can be left or right, doesn’t matter)

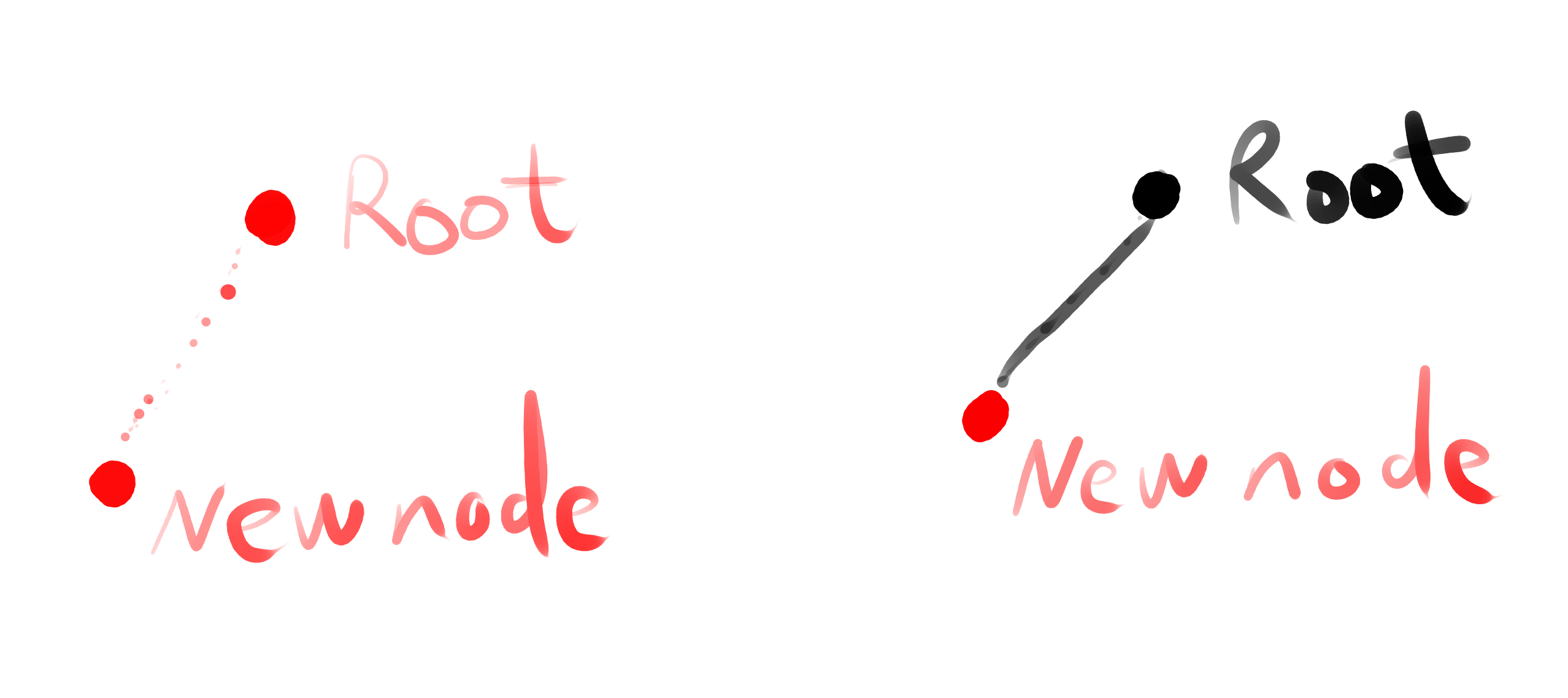
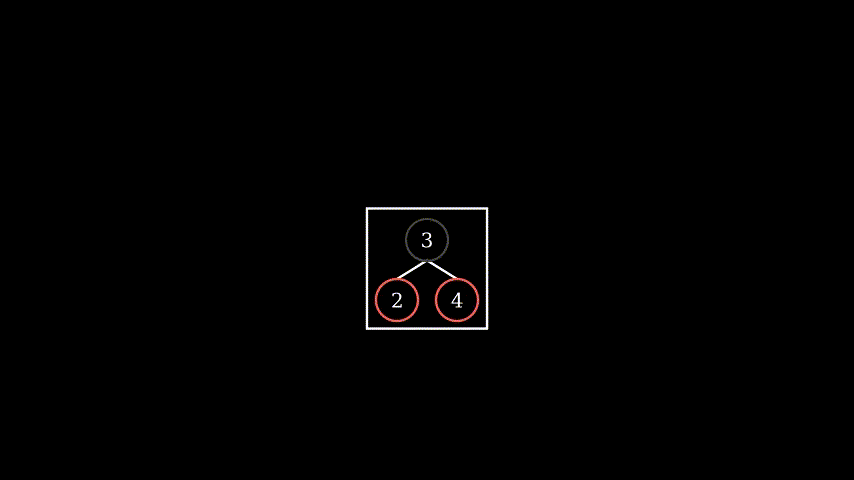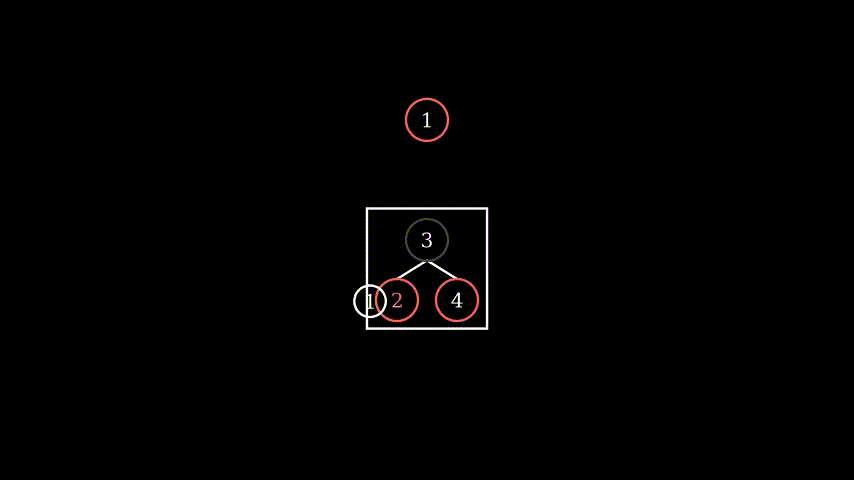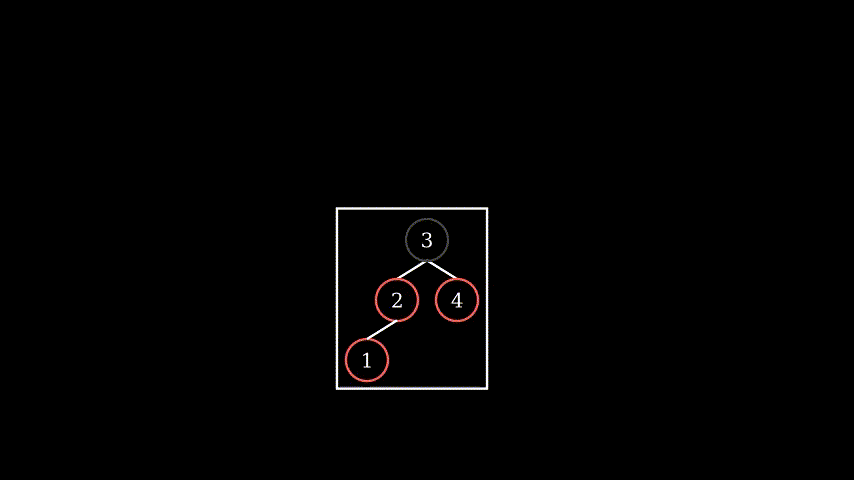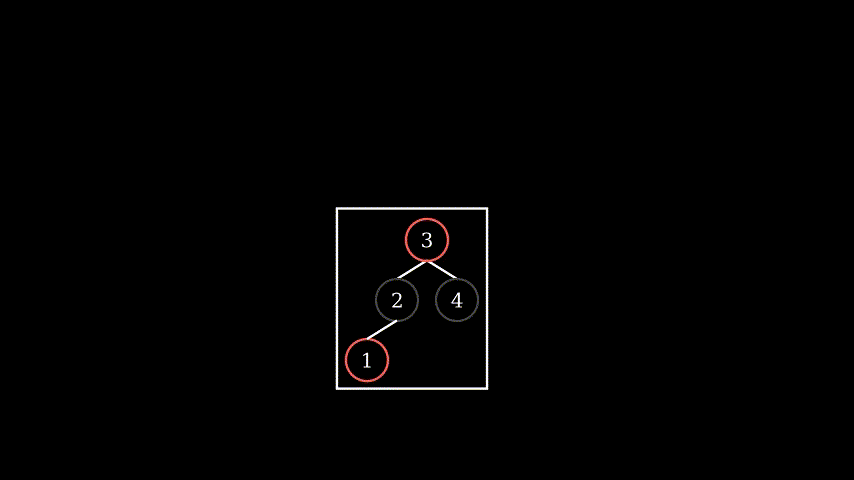
3.1 if uncle doesn’t exist, we rotate at grandparent node like following: (in animation, we use gray color for black node)

if new inserted node stay between parent and grandparent, first rotate at parent level, make it same as first variant

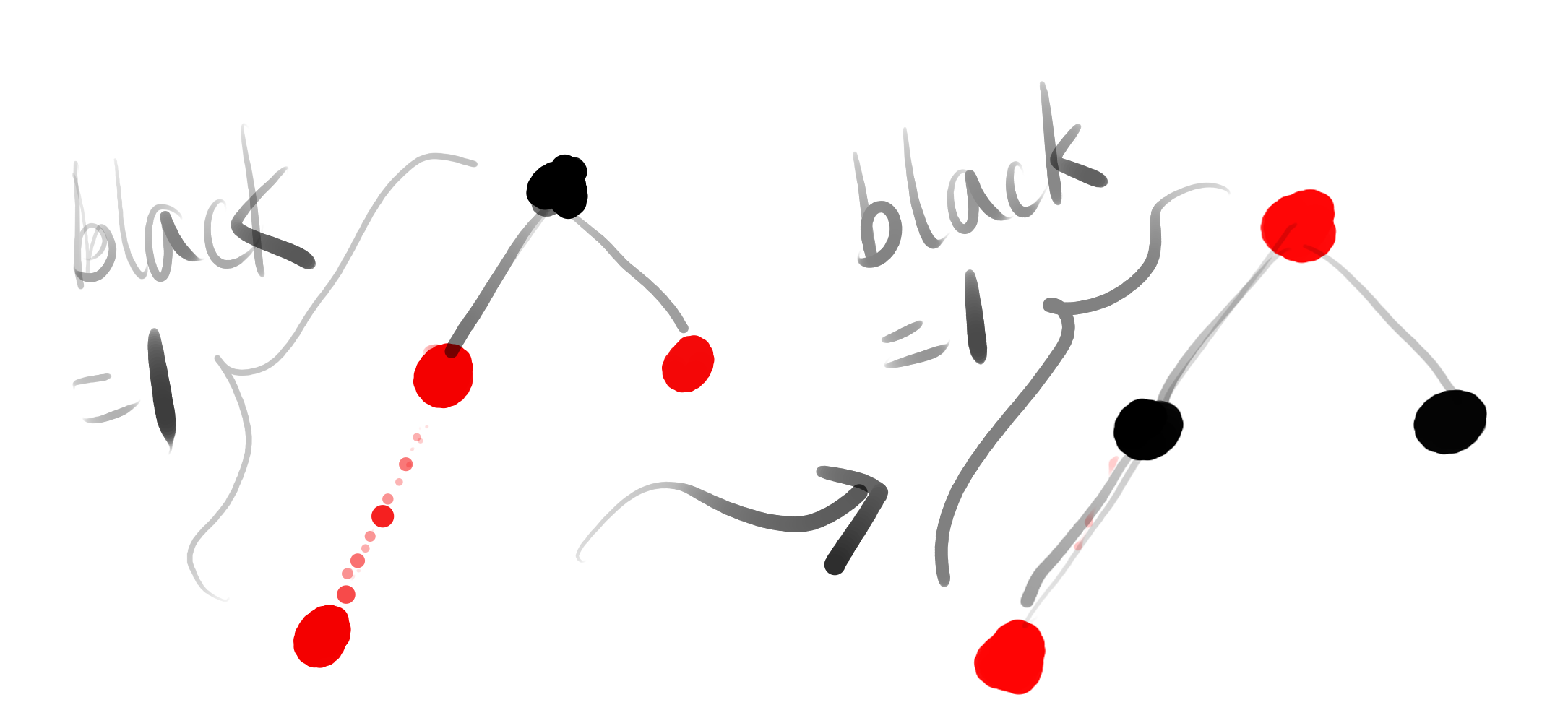
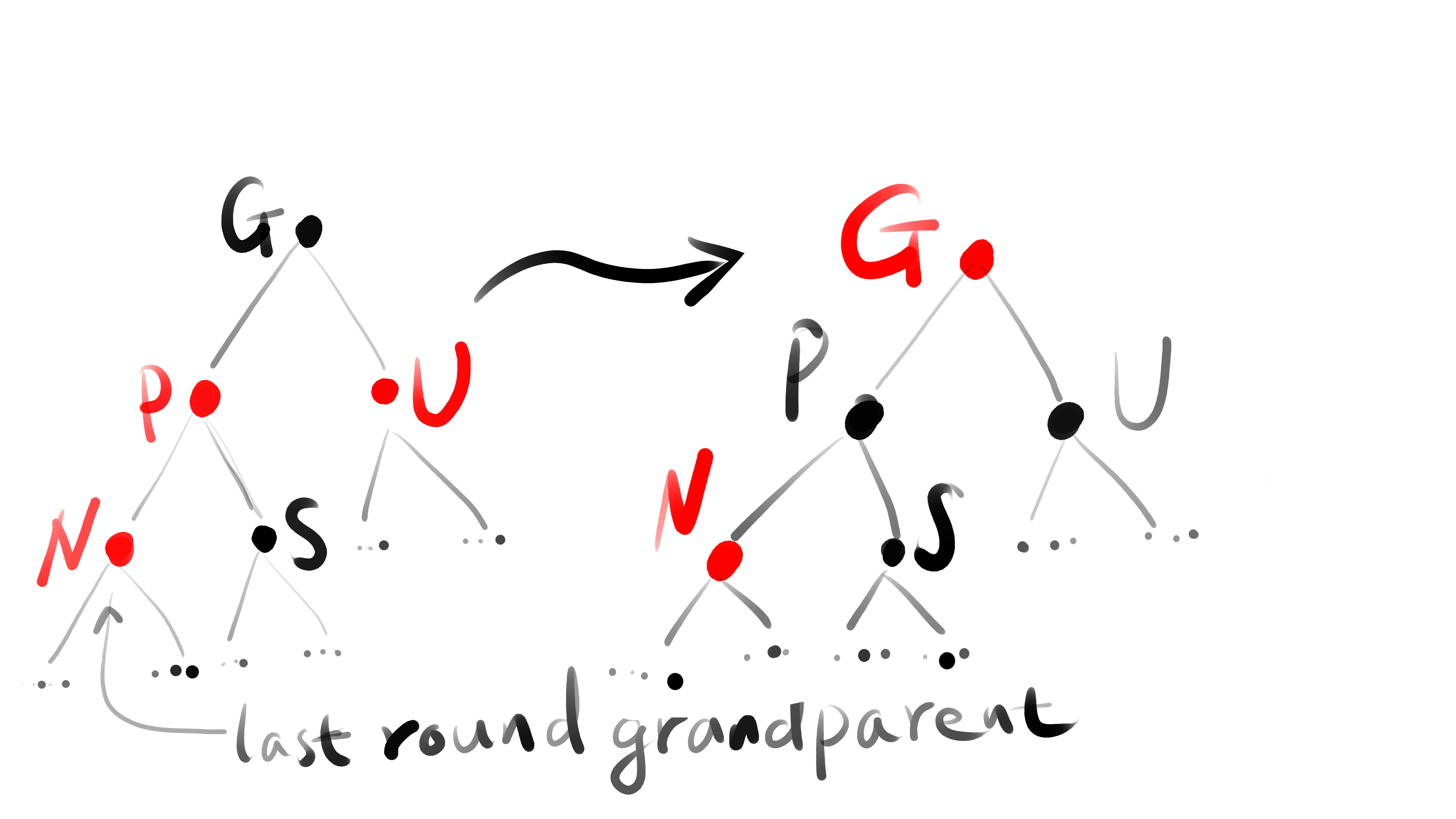
3.2 if uncle exist, then it must be RED (otherwise breaks black height rule). For such situation, we color Grandparent as red, P/U as BLACK (so the black height), then sub-tree under grandparent is fixed, but if grandgrandparent is red, it’s possible to lead consequent red with grandgrandparent so we need recursively fix it. Then we treat G as ‘new inserted node’

before and after transform comparison: higher sub-tree became valid, black height stay unchanged, potential consequent red problem pushed upwards

condition 3.1/3.2 only consider the first iteration (insert node is leaf) condition, during recursive, it’s possible to see different variants of 3 (note, we only need further fixing under condition 3.2, so next recursive we’ll always see the ‘lowest changed node’ as RED). If new parent is black then fixed completed, just like condition 1 (since 3.2 won’t change black height)

4.1 if new red parent is the root, then turn root into black, so tree black height finally increase one. Since changed sub-tree always maintain exactly same black height as before insertion, equals to its sibling, so black height equal rule never breaks

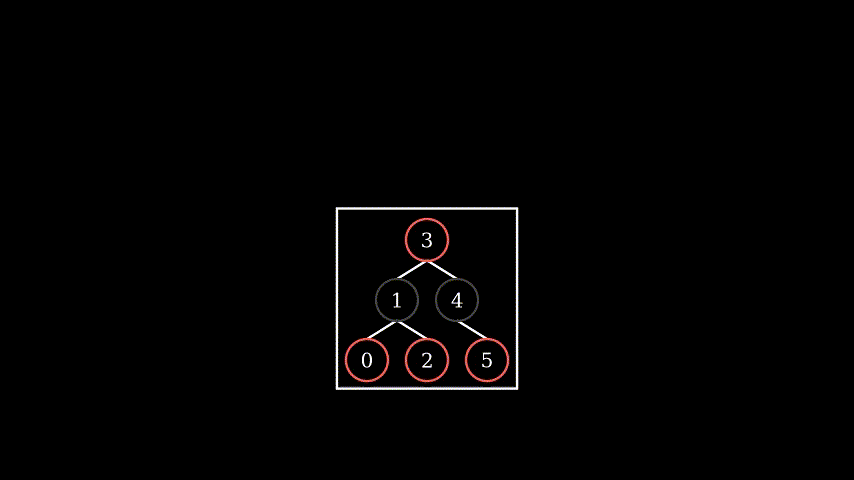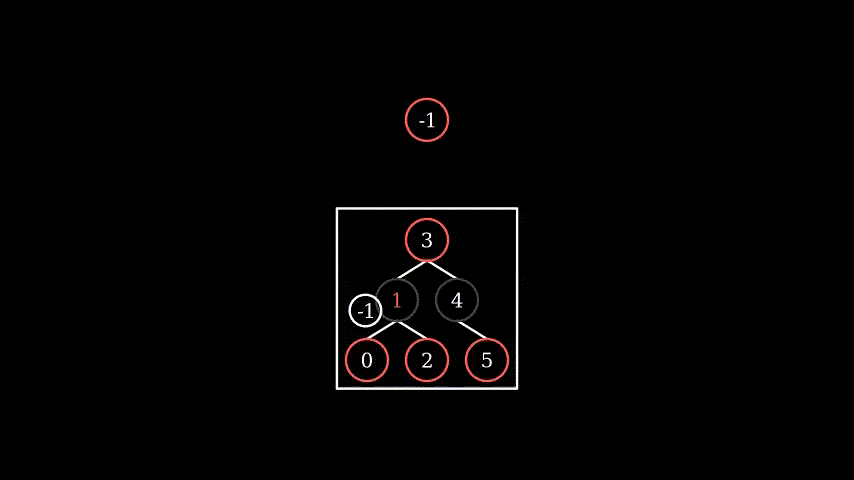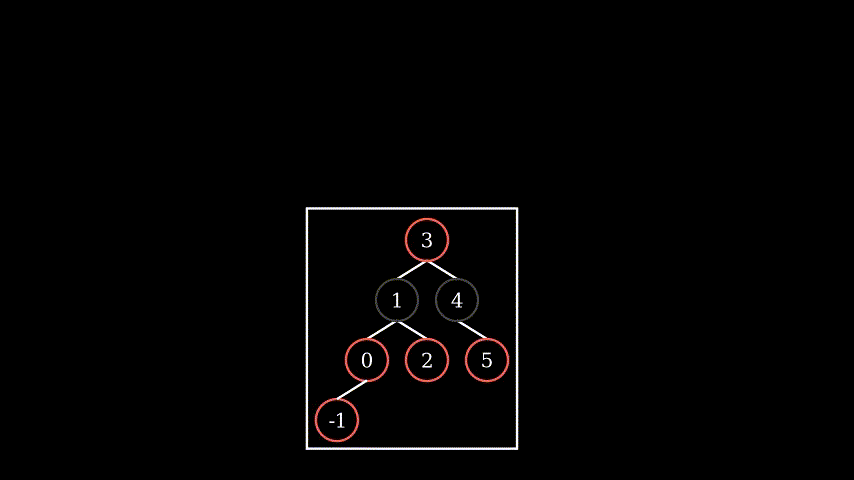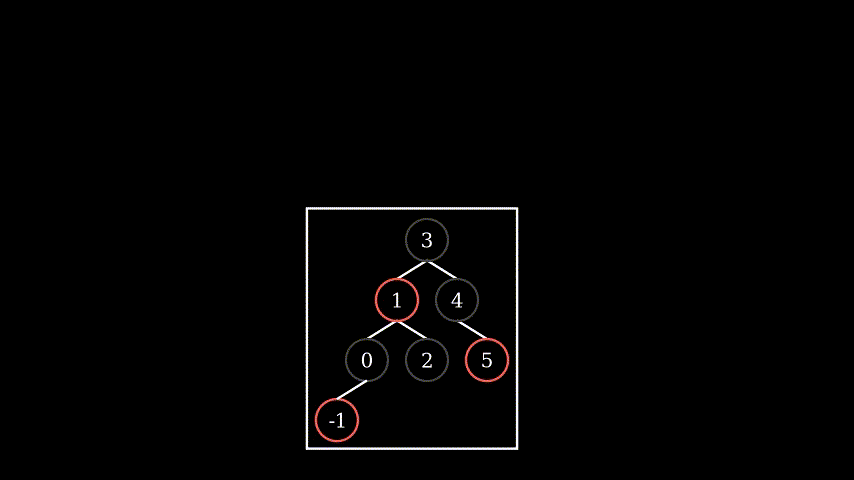
4.2 similar to 3.2, just with more sub-tree (apply 3.2 fix and then recursive)

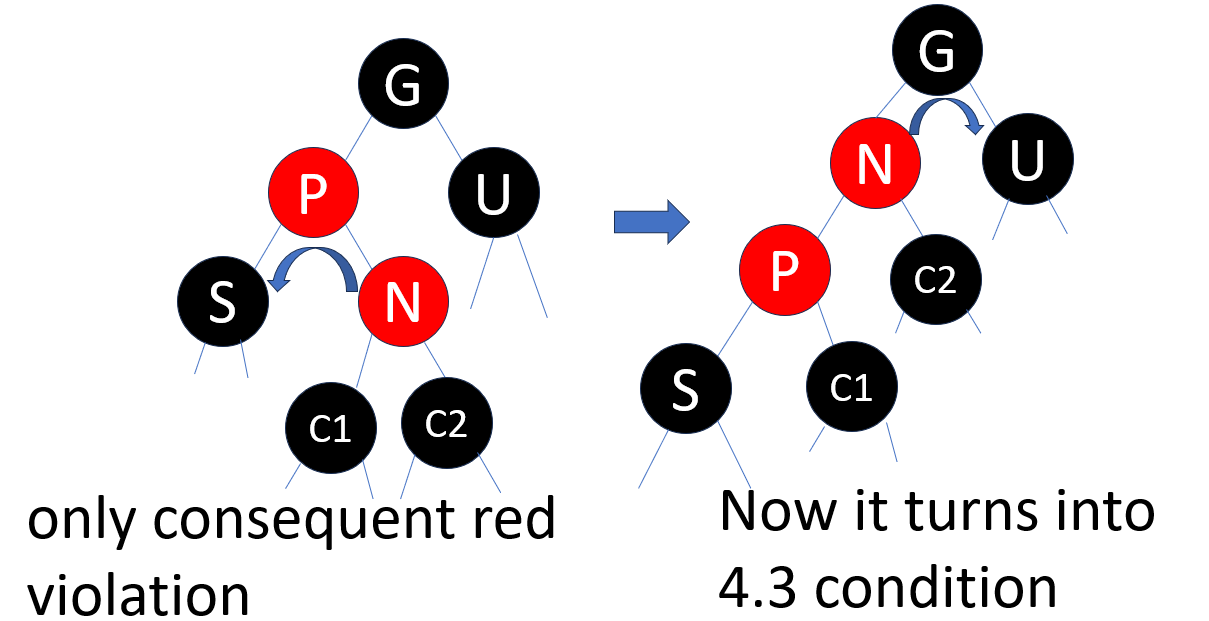
4.3 if new parent is not root, uncle is BLACK, sit far away to new appeared RED node

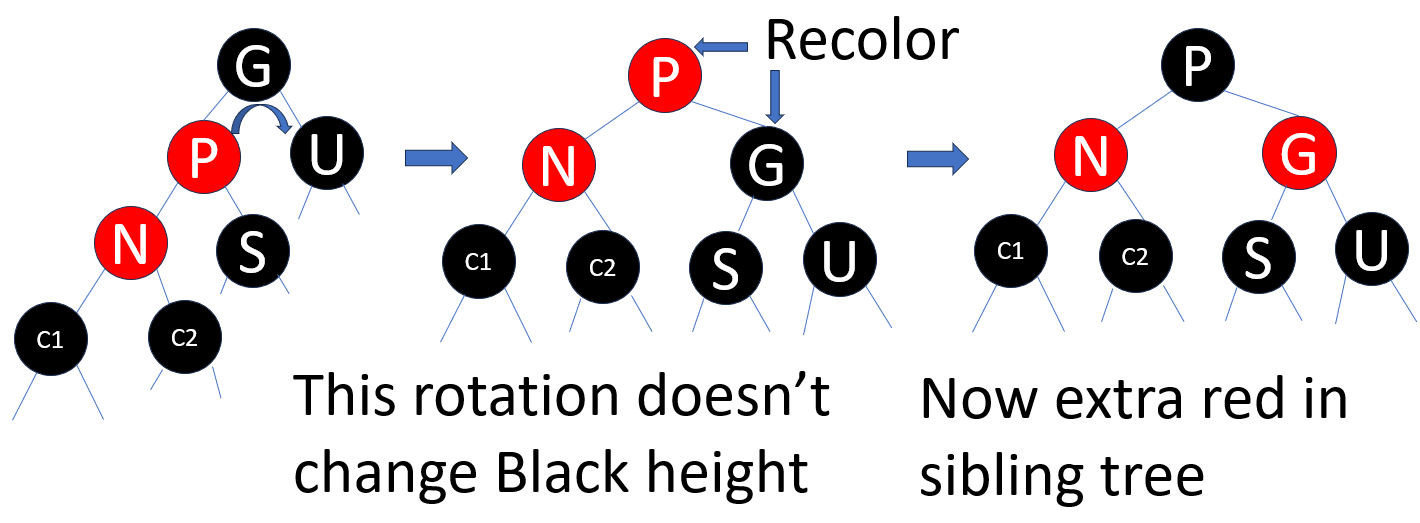
in this diagram, left sub-tree has too many red node which can’t fit , and we know uncle tree have black-black (G-U) structure, so we push that red color to uncle tree left state (before fixing), every subtree is already balanced, N(R), S(B), U(B) all have same black height, so after moving S as G child, G(R) is also balanced and path at N(R) changed from B->R->R to B->R, black height also unchanged, thus after fixing, P is balanced. since it’s Black, so no further fixing required

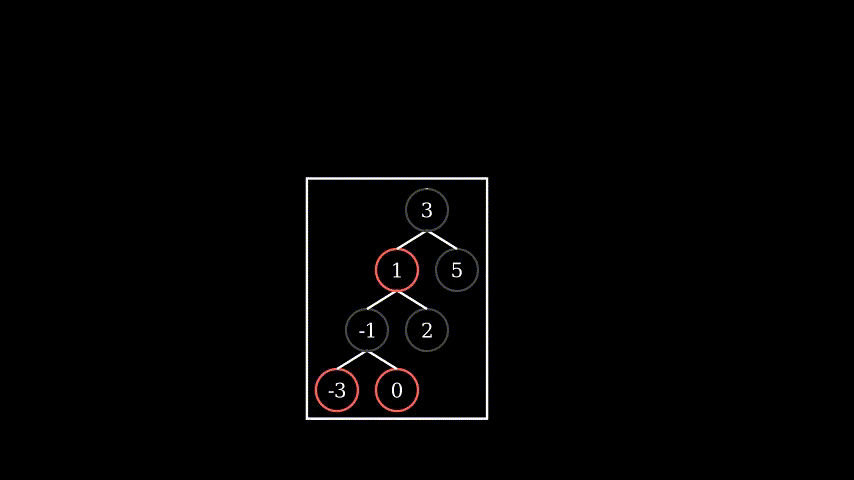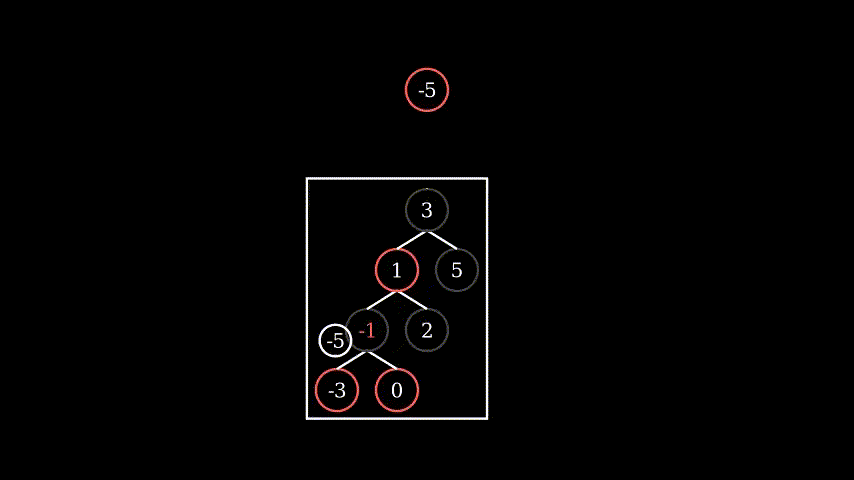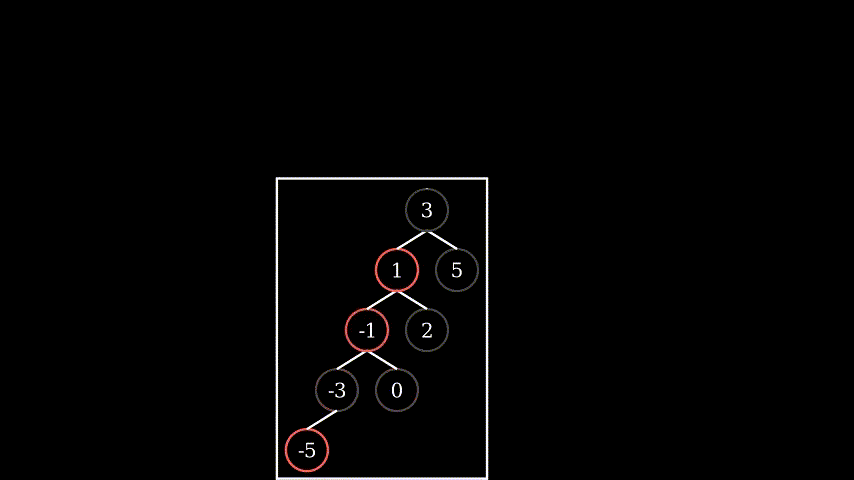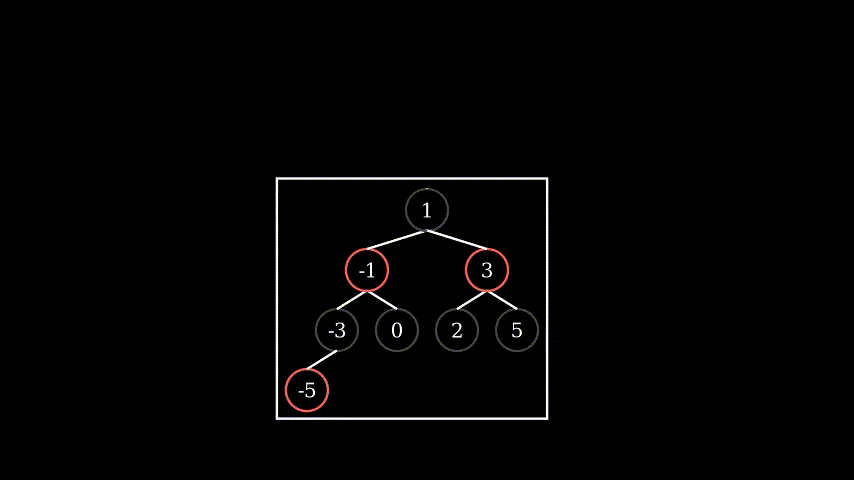
4.4 similar to 4.3, but new appeared RED and uncle near each other, so we have

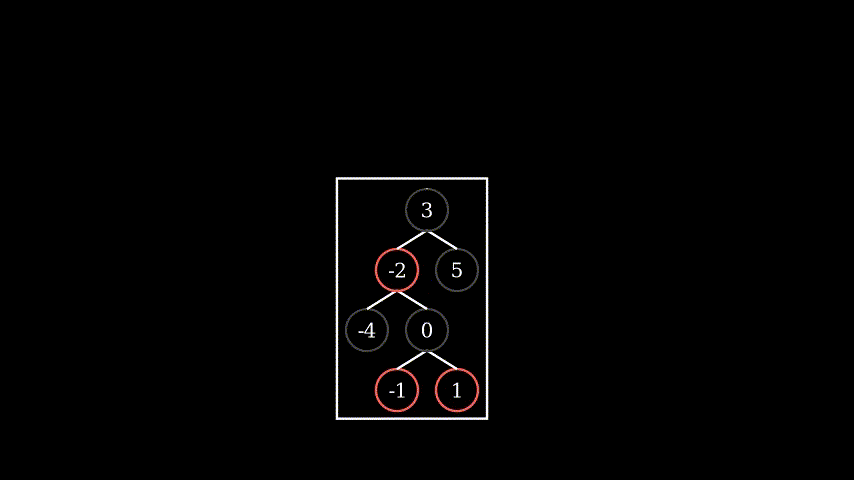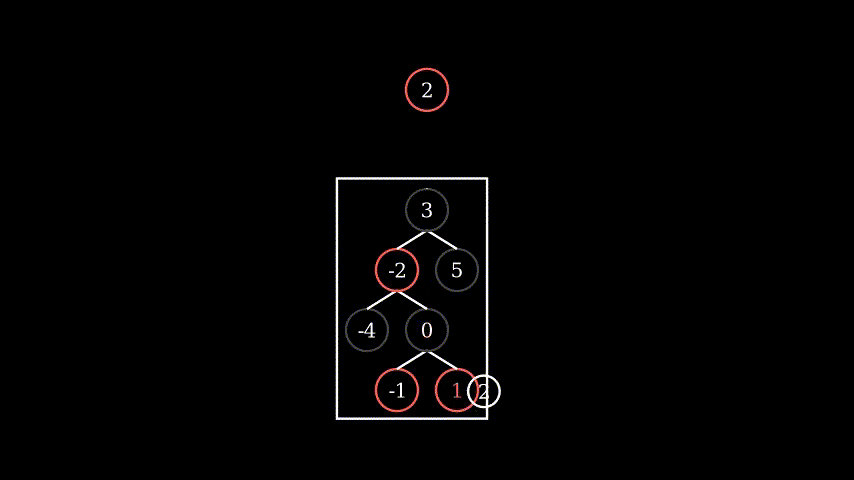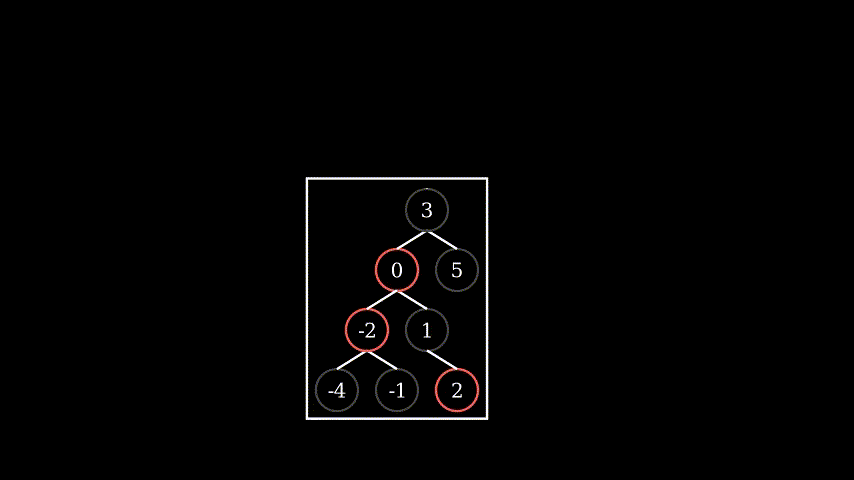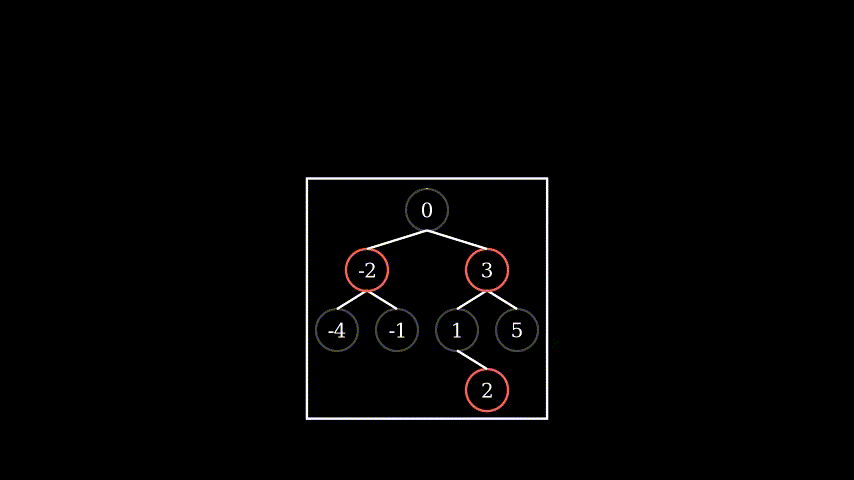
That’s all possible conditions to fix after insertion.

note it’s possible to fix violation by other way. By RED-BLACK tree definition, it shouldn’t be too hard to prove that for a sub-tree with black height = N, the max depth is 2N + 1 depth (N black + N + 1 RED) which can hold total nodes T = 2 ^ (2N + 1) , RED nodes R = 2/3 T, BLACK nodes B = 1/3 T or B = (T- 1) /3 , R = 2 B + 1 (if T can’t be dived by 3). so we can check along ancestors to tell if it can hold extra color and construct whole sub-tree, which can also be valid fixing, just not most optimal.

For deletion the basic idea still stay the same : try to re-arrange nearby nodes to fix violation, if not possible, then try to make higher sub-tree valid, push the problem upwards. And important point: we’re not deleting target node directly, we always delete the switched in-order successor as BST.

so our deletion steps:

swap target node with in-order successor node, then deleting the swapped node. then the problem turned into delete a leaf node, or a node with right only child (because the in-order successor is leftmost of right sub-tree).

remember RBTree property 1: if the node to delete is red, it doesn’t affect black height, neither will introduce consequent red violation, and according to RBT property 2, it also can’t contain one child, so it will be the simplest condition, just remove it

the deletion node is red condition: P (BLACK)
/
D Red

now left conditions is to delete a black node, which will decrease its path black height, but there’s an interesting fact which actually make RB-Tree deletion much easier to understand: if there’re one nearby red node, no matter if it’s the child, parent, sibling, or nephew it’s always possible to re-arrange nearby nodes to ‘move’ that red to deleted node path, then color it black to restore the decreased height , so problem resolved locally

3.1 use child red to restore black height:

 P (can be red or black)   P (color doesn't change)                       
 /       \                 /              \         
D (black) S(BLACK)  =>   C (black)         S(BLACK) 
 \                                                  
  C (red)                                           

3.2 use parent red to restore black height:

   P (RED)                                P(BLACK)     
  /       \               ====>                  \        D (BLACK)   S(BLACK)                               S(RED)

3.3 use sibling red to restore black height (so parent must be black) P (BLACK) S(BLACK) / \ /
D(BLACK) S(RED) =====> P(RED) N2(BLACK) / \ / \
N1(BLACK) N2(BLACK) D(BLACK) N1(BLACK) N1/N2 must exist because equal black height rule

this is not re-balanced, but now it turned to be same situation as 3.2, 
or one of 3.4~3.6

3.4 the only nephew is red and far away(so sibling must be BLACK)

  P (can be RED or BLACK)                     S(color as P original color)
      /         \                              /              \
 D(BLACK)       S(BLACK)          ==>   P(turned to BLACK)     N (turned to BLACK)
                   \
                    N(RED)

3.5 only nephew is red and nearby (so sibling must be BLACK)

  P (can be RED or BLACK)                     P(can be RED or BLACK)
      /         \                              /              \
 D(BLACK)       S(BLACK)          ==>   D(BLACK)       N (turned to BLACK)             =>    now can be handled as 3.4
                /                                               \
             N(RED)                                              S(turned to RED)

3.6 both nephew is red: (so sibling must be BLACK)

  P (can be RED or BLACK)                     S(color as P original color)
      /         \                              /                \
 D(BLACK)       S(BLACK)          ==>   P(turned to BLACK)       N2 (turned to BLACK) 
                /     \                        \                    
             N1(RED)   N2(RED)                  N1(RED)            

then all cases listed in 3 is resolved, they keep same black height as before deletion, and these transform won’t introduce consequent red violation to sibling nor parent, so RB-tree already being fixed.

then what left is ‘too many black’ condition, no red nodes as child/parent/sibling/nephew

4 this is the only possible condition for first step process

P (B) P(B) / \ ==>
D(B) S(B) S(R)

during processing in 4, although we didn’t restore the black height, but make one-level-more sub-tree re-balanced, that said, we ‘push’ the ‘black height decrease 1’ condition upwards. as we see in 4, root node of fixed sub-tree are always black (because all condition with nearby red node in sub-tree can be resolved without requiring further fixing), so from higher level node’s perspective, it’s nothing changed in that sub-tree (lowest node still black) except its black height decrease 1, so it’s exactly same as we delete one black node in first iteration (both deletion node and that sub-tree root is black, so all color based triaging and assumption still applied) then transform in 3 and 4 can be applied again, until we found nearby RED child, or reach the ROOT (whole tree black height deceased one).

the differences is that during recursive, we will have some variants of previous conditions (due to changed branch now have child sub-tree) and we won’t use red color from child anymore (if current lowest child has a red node which exists before previous round, then it should already being used to fix the tree, so only possibility is that red node is introduced to rebalance current lowest child sub-tree, which can’t be moved otherwise sub-tree became imbalance again)

so 3.1 not applied anymore 3.2 ~ 3.6, nothing changed except the node is not for deletion, still attached with it’s parent, RBT fixed complete

4 will have one more variant:

   P (B)                                   P(B)
  /    \                                 /     \
L(B)   S(B)               ===>         L(B)     S(turned to RED)
/\      /  \                           / \      /  \    ......  N1(B) N2(B)                    ...     N1(B) N2(B)   (note: N1 and N2 must be black, since any red nephew condition is handled by 3.4~3.6)   we turn it into balanced valid RB-Tree, also pushing 'black height decrease 1' condition upwards

now all condition in deletion being discussed, some simplest condition omitted, like insert/delete as root. and to achieve sub-tree rebalance, there can be different transform applied, let’s say

         P(R)                                          S(B)                         S(R)
        /   \                                         /   \                         /  \
     L(B)   S(B)    can be transformed to           P(R)   N2(R)  , or also      P(B)   N2(B)
     /     /   \                                    /  \     \                   /  \      \
         N1(B)  N2(R)                           L(B)  N1(B)  ...               L(B)  N1(B)  ...
                 \ both transform are valid,  but 2 is preferred, because P turned to BLACK, also allow N1 with red color to be attached which can help simplifying the code

I hope this blog can help you understanding RB-Tree

I encourage readers to implement it themself. Personally I can’t write a correct implementation without understanding the basic idea, neither did I can fully understand the details without finishing the implementation(which also means fixing all the bugs).